תצטרכו 10 מיליארד שנה להבין את הפתרון המתמטי הזה
מחשב על הצליח לפתור בעיה מתמטית בת 30 שנה בתחום משפטי פיתגורס. אולם מדובר בהוכחה כל כך מורכבת שבדיקתה אינה אפשרית למוח אנושי
פתרון של בעיה מתמטית שהציג המתמטיקאי האמריקני רונלד גרהאם לפני כ-30 שנה בתחום משפטי פיתגורס נמצא לאחרונה על ידי שימוש במחשב על. חוקרים מארצות הברית ומאנגליה, הם שפרסמו בחודש מאי את ההוכחה המתמטית הארוכה הזו שנחשבת לארוכה ביותר שנכתבה עד כה כך מדווח עיתון הכרוניקל.עם זאת מדובר בפתרון מתסכל שנראה כי לא ניתן יהיה לעבור עליו ולבדוק את דרך הפתרון הממוחשבת הזו וזאת משום האורך האדיר של ההוכחה שנעשתה על ידי המחשב. מדובר בכמות חישוב המשולה ל10 מיליארד שנות אדם. מבחינה זו מדובר בפתרון מתסכל מאד מבחינה מדעית כיוון שהוא אינו אפשרי להבנה. להמחשה באתר מכון דוידסון למדע, הזרוע החינוכית של מכון ויצמן, מסבירה החוקרת מירי אדלר כי "ההוכחה היא קובץ שגודלו כ-200 טרה-בייט. משמעות הדבר היא שכדי להוריד את ההוכחה תצטרכו לצרוב כ-280,000 דיסקים".
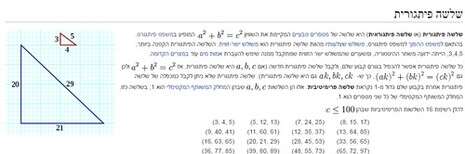
הסבר על שלשות פיתגוריות
צילום מסך מתוך ויקיפדיה
- כל התכנים הכי מעניינים - בעמוד הפייסבוק שלנו
השאלה שנפתרה
השאלה שפתרו החוקרים היא "בעיית השלשות הפיתגוריות", שהמתמטיקאי האמריקאי רונלד גרהם ניסח בשנות השמונים. שלשה פיתגורית היא קבוצה של שלושה מספרים (a, b, c) המקיימים את הקשר המוגדר במשפט פיתגורס: a2 + b2 = c2. למשל: 3, 4, 5 הם שלשה כזו (9+16=25). גרהם שאל אם אפשר לחלק סט של מספרים טבעיים (שלמים וחיוביים) מ-1 עד N לשתי קבוצות כך שאף אחת מהן לא תכלול שלשה פיתגורית. גרהם אף הציע פרס של 100 דולר למי שיפתור את הבעיה, ואכן נאלץ להעניק את הסכום הזה לקבוצה שפתרה אותה כעת.
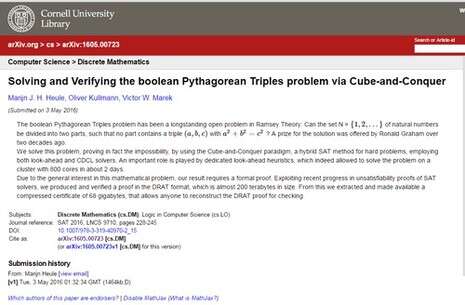
ההודעה על הפתרון
צילום מסך
המתמטיקאים שהציגו את הפתרון הם מארין יול (Heule) מאוניברסיטת טקסס, ויקטור מארק (Marek) מאוניברסיטת קנטקי ואוליבר קולמן (Kullmann) מאוניברסיטת סוונסי הבריטית. השלושה הוכיחו שיש פתרון לבעיה עד למספר N = 7,824. כלומר, את אוסף המספרים שבין 1 ל-7,824 אפשר לחלק לשתי קבוצות כך שבכל קבוצה אין שום שלשה פיתגורית.
במאמר שפורסם בינתיים רק באתר הפרסום המקדים Arxiv, הם גם הוכיחו כי בעבור N = 7,825 כבר אין פתרון, ואי-אפשר לחלק את קבוצת המספרים בלי לכלול שלשה פיתגורית באותה קבוצה. מספר אפשרויות הפתרון לבעיה היה כה גדול שסקירת האפשרויות השונה הייתה אמורה להימשך כ-35,000 שעות (כמעט ארבע שנים) בכוח חישוב קונוונציונלי. אך בעזרת מחשב-על של אוניברסיטת טקסס, ובו 800 מעבדים שחישבו בו-זמנית, הצליחו החוקרים לסיים את החישוב ביומיים בלבד.
היכנסו לעמוד הפייסבוק החדש של nrg